P、NP、NP-hard、NP-compelet(NPC)
P、NP,P=NP?
P问题指能在多项式时间内解决的问题
NP问题指一个给定问题的解,能在多项式时间内验证这个解正确与否的问题
P问题属于NP问题,所有P问题都是NP问题。因为能在多项式时间内解决一个问题则必定可以在多项式时间内验证一个问题的解
但是P是否等于NP是一个还未得到验证的问题,就是说没有人能证明是否所有NP问题都是P问题。但是,一个总的趋势、一个大方向是有的。人们普遍认为,P=NP不成立,也就是说,多数人相信,存在至少一个不可能有多项式级复杂度的算法的NP问题。
NP-hard和规约
规约是指:如果问题A问题能用B问题的算法解决,则A问题可以规约为B问题,且B问题难于A问题。如解一个一元一次方程可以用一元二次方程的算法解决。(把A问题的输入变换一下输入到B问题中,能得到A问题的答案)
所有的NP问题都可以规约为这个问题,则这个问题是NP-hard,但是这个问题不一定是NP问题(区别于NPC问题)
NPC
NPC问题是同时满足如下条件的问题:
- 它是一个NP问题
- 所有的NP问题都能规约到它
即一个既是NP问题又是NP-hard问题
证明一个问题是NPC问题也很简单。先证明它至少是一个NP问题,再证明其中一个已知的NPC问题能规约到它。
既然所有的NP问题都能规约成NPC问题,那么只要任意一个NPC问题找到了一个多项式的算法,那么所有的NP问题都能用这个算法解决了,NP也就等于P了。因此,给NPC找一个多项式算法太不可思议了。因此,前文才说,“正是NPC问题的存在,使人们相信P≠NP”。我们可以就此直观地理解,NPC问题目前没有多项式的有效算法,只能用指数级甚至阶乘级复杂度的搜索。
用图灵机解决最大割问题
通常所说的图灵机都是确定型图灵机。非确定型图灵机和确定型图灵机的不同之处在于,在计算的每一时刻,根据当前状态和读写头所读的符号,机器存在多种状态转移方案,机器将任意地选择其中一种方案继续运作,直到最后停机为止。
能用确定图灵机在多项式时间内解决的问题是P问题。
能用非确定图灵机在多项式时间内解决的问题是NP问题。
最大割问题和分析
最大割問題(英语:Maximum Cut)是 NPC问题。給定一张图,求一种分割方法,将所有定点(Vertex)分割成两群,同时使得被切断的邊(Edge)数量最大。
如G(E,V)是如下的无向图,包含v1,v2,v3,v4四个点,我们给出这个问题的解为3,验证这个答案对不对。(NP问题)显然这个答案是正确的,比如我们将顶点集合V分成S、T两个子集S = {v1,v4} et T ={v2,v3}.
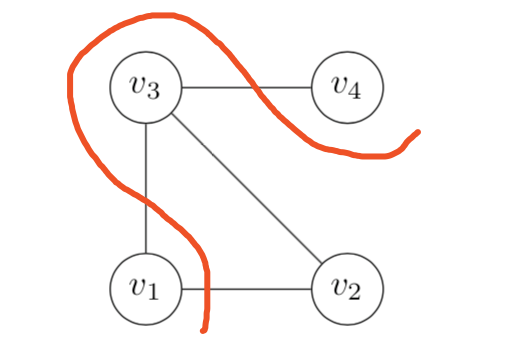
显然我们找不到割为4的解法。
复杂度
要解决这个问题,首先我们分析它的复杂度。
这个问题实际上是将一个图的顶点集合分成两个子集的问题,分成两个子集之后再看这两个顶点子集之间存在多少条边,最大边数的分割方式就是问题的解。
一个顶点可能属于子集A也可能属于子集B,每个顶点就有两个可能性,若这个图有n个顶点,这个问题复杂度至少为O(2^n),为指数级。但是给出这个问题的解来验证解的正确性是多项式范围内的,所以我们用非确定性自动机来解决这个问题.

图灵机
一个纸带,四个读写头绿色蓝色红色黑色。绿色和蓝色来表示分割的子集,红色读取矩阵值,黑色写结果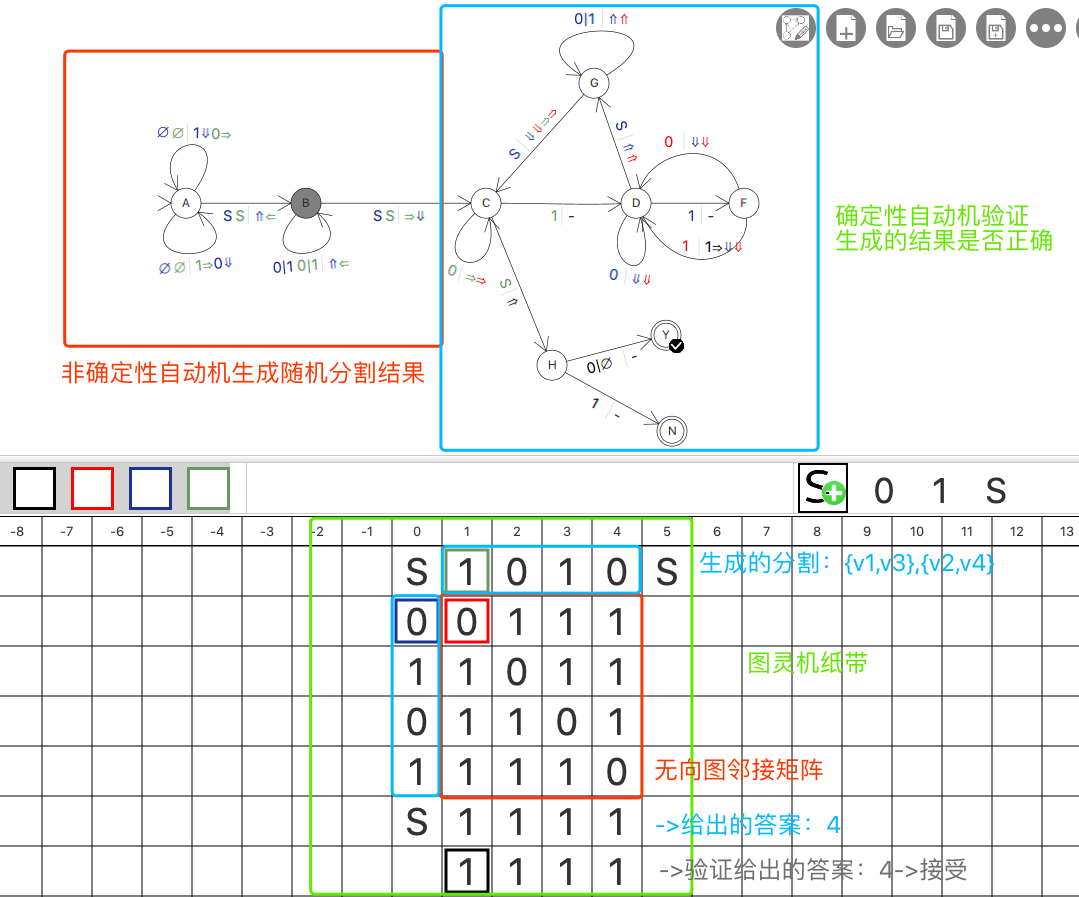
验证答案正确性的复杂度:O(n^2)