TreeMap 继承于AbstractMap,实现了navigableMap, treeMap是红黑树的java实现,已经分析过,红黑树能保证树的增删改查都在O(logN).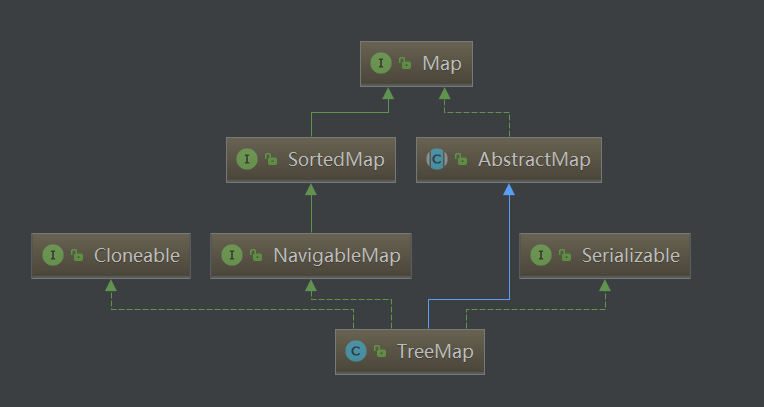
1 | public class TreeMap<K,V> |
成员变量
类型为键值对的根节点
树的大小
修改次数modCount,这个变量记录了对象的修改次数,再Iterator中使用,Iterator中有变量expectedModCount也记录了对象的更改次数,在遍历的时候若expectedModCount和modCount不同则说明有其他线程已经修改了这个对象,抛出异常。
modCount通常在线程不安全的类中才会看到,是一个避免多线程操作错误的方式:fast-fail策略。所以当大家遍历那些非线程安全的数据结构时,尽量使用迭代器。
1 | //final,声明后不可改变 |
- 这个类实现了Serializable接口,可序列化,transient关键字可以避免有该关键字的变量不被保存,默认情况下,对象中的所有变量都转换为持久状态。 在某些情况下,我们可能想要
避免保留一些变量,因为没有必要通过网络传输。
Entry
Entry其实就是树的节点,一个键值对,这里的节点保存着key,值和父节点,左孩子,右孩子和节点颜色(初始颜色黑色),还有一些修改节点,获得值的方法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15static final class Entry<K,V> implements Map.Entry<K,V> {
K key;
V value;
Entry<K,V> left;
Entry<K,V> right;
Entry<K,V> parent;
boolean color = BLACK;
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
// ... 省略其他方法
}
构造函数
四个构造函数
默认构造起使用默认的自然比较, 也可以指定特殊的比较器
1 | // 默认构造,比较器采用key的自然比较顺序 |
方法
添加元素
像红黑树增加一个元素:
1 | public V put(K key, V value) { |
左旋转:
1 | /** From CLR */ |
获取元素
TreeMap中的元素是有序的,当使用中序遍历时就可以得到一个有序的Set集合,所以获取元素可以采用二分法:
1 | final Entry<K,V> getEntry(Object key) { |
获取前一个元素
1 | static <K,V> Entry<K,V> predecessor(Entry<K,V> t) { |
暂时分析到这里,其他复杂方法先暂时不研究了。。