[算法]-排序算法

发表于 | 分类于 | 阅读次数

初级排序

选择排序

选择排序：找到数组中最小的和第一位交换位置，再从剩下的元素中找到最小的和第二个元素互换位置，一支往复到整个数组排序完成。类似于拿到一手杂乱的牌整牌的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static<T extends Comparable<T>> void SelectionSort(T[] list){
    int len = list.length;
    int i,j,minJ=0;
    int min;
    for(i=0;i<len-1;i++){//n-1次比较
        min=i;
        for (j=i+1;j<len;j++){//len-i
            if(list[min].compareTo(list[j])>0){
                min =j;
            }
        }
        T tmp = list[min];
        list[min] = list[i];
        list[i] = tmp;
    }
}

复杂度

大约要比较N^2/2次， 进行N次交换，复杂度O（n^2）

插入排序

插入排序是将元素插入一个已经排序的序列的适当位置，相当于一边起牌一边整理手中已经排序了的牌.举个栗子，对5,3,8,6,4这个无序序列进行简单插入排序，首先假设第一个数的位置时正确的，想一下在拿到第一张牌的时候，没必要整理。然后3要插到5前面，把5后移一位，变成3,5,8,6,4.想一下整理牌的时候应该也是这样吧。然后8不用动，6插在8前面，8后移一位，4插在5前面，从5开始都向后移一位。注意在插入一个数的时候要保证这个数前面的数已经有序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static<T extends Comparable<T>> void InsertionSort(T[] list){
    int len = list.length;
    int i,j;
    for (i = 1; i<len; i++){//只有一张牌的失衡不用排序，从第二张开始往前插入
        for (j=i;j>0;j--){
            //将list[i]这张牌插入，如果比前一张牌小就交换位置，直到找到合适的位置（大于前一张牌小于后一张牌）
            if (list[j].compareTo(list[j-1])<0) {
                exchange(list,j,j-1);
            }
            else
                break;
        }
	}
}

复杂度

这个排序方式复杂度取决于数据的有序性，如果已经是大致有序数组就会效率比较高。

但依旧是O（n^2）,对于随机数据选择排序和插入排序表现差不多。

希尔排序是对插入排序的改进，移步：https://segmentfault.com/a/1190000013967025

希尔排序的性能甚至不差于高级排序，且代码量少，且不需要额外的内存空间。算法第四版给出了一个性能不错递增序列：{1,4,13,40,121,364…}

希尔排序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static<T extends Comparable<T>> void ShellSort(T[] list){
    int len = list.length;
    int i,j;
    int h =1;
    while (h<len/3)
        h=3*h+1;
    while (h>=1) {
        for (i = h; i < len; i++) {
            for (j = i; j >= h; j -= h) {
                if (list[j].compareTo(list[j - h]) < 0) {
                    exchange(list, j, j - h);
                } else
                    break;
            }
        }
        h/=3;
    }
}

冒泡排序

1
2
3
4
5
6
7
8
9
10
11
12
13

public static<T extends Comparable<T>> void BubbleSort(T[] list){
    int len = list.length;
    for (int i = 0;i<len-1;i++){
        for (int j = 0;j<len-i-1;j++){//进行n-1次冒泡比较，每次将最大的数字冒到上方
            if (list[j].compareTo(list[j+1])<0){//比较相邻元素，交换位置
                T tmp = list[j];
                list[j] = list[j+1];
                list[j+1]=tmp;
            }
        }
    }
}

归并排序

将元素分为两半分别排序再将结果归并起来，归并排序能将任意长度为N的数组的排序时间和NlogN成正比，但是他需要额外的N正比的存储空间。

O(logN)

自顶向下的归并排序

自顶向下就是从整个的数组，变成小数组，分成小问题来解决，也就是递归。

我们首先定义将两段有序数组归并的函数merge。

归并排序是一个分治思想，用递归实现。一个数组被分成左右两边进行排序，左右两边有能继续划分左右，直至左右两边都只有一个元素。分成两组后，将链遍分别排序之后用merge函数合并（实际上排序被划分为两个数字比较的子问题）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
static Comparable[] copy;

private static<T extends Comparable<T>> void merge(T[] list, int lo, int mid, int hi){//将一个两边分别排序了的数组归并
    for(int k = lo; k<=hi; k++){  //将数组复制
        copy[k] = list[k];
    }

    int i = lo, j =mid+1;//i,j分别表示前后两段的起始

    for(int k=lo; k<=hi;k++){
        if(i>mid){//左边已经没有元素了
            list[k] = (T)copy[j];
            j++;
        }
        else if(j>hi) {//右边没有元素了
             list[k] = (T)copy[i];
             i++;
        }
        else if(copy[i].compareTo(copy[j])<0){
            list[k] = (T)copy[i];
            i++;
        }
        else {
            list[k] = (T)copy[j];
            j++;
        }

    }
}

public static<T extends Comparable<T>> void MergeSort(T[] list){
    copy = (T[])new Comparable[list.length];
    MergeSort(list,0,list.length-1);
}

public static<T extends Comparable<T>> void MergeSort(T[] list,int lo, int hi){
    if(lo>=hi)
        return;
    int mid = lo+(hi-lo)/2;  //将数组分成左右两边
    MergeSort(list, lo, mid);  //对左边继续划分排序
    MergeSort(list, mid+1,  hi); //对右边划分排序
    merge(list,lo,mid,hi);
}

自底向上的归并排序

相对于自顶向下的分治，自底向下是从小问题到大问题。我们先22归并，在44归并，88归并。。直到最后，可能最后一次归并后半段数组长度比前半段小

1
2
3
4
5
6
7
8
9
10
public static<T extends Comparable<T>> void MergeSort2(T[] list){
       copy = (T[])new Comparable[list.length];
       int i,lo;
       for(i=1;i<list.length;i+=i){
           for(lo = 0;lo<list.length-i;lo +=i+i){
               merge(list,lo,lo+i-1, Math.min(lo+i+i-1,list.length-1));
           }

       }
   }

快速排序

快速排序是原地排序（只需要一个很小的辅助栈），且内循环短小，所以无论是理论上还是实际中他都更快一些。复杂度O(logN)。

快速排序也是分治的思想，用递归来实现。每一轮排序我们将一个元素位置排定，即它的左边元素都比它小，右边的元素都比它大，数学归纳法可知N次排序能将所有的元素排好顺序。每一轮排序我们选定一个要排定的元素，通常选择list[lo]，j是最右边的元素，j向左走，当遇到比list[lo]小的元素停止，i从最右边出发，遇到比list[lo]大的数字停止，i和j互换元素。然后继续，还是j先出发，遇到比list[lo]小的数字停止，i开始出发。。。这样继续直到i和j相遇，将list[lo]和相遇位置的元素互换位置，这一轮结束，我们称这个过程为切分partition。然后利用递归将该元素左边的数组和右边的数组也进行如此切分，直到全部有序。

快速排序最好的性能是每次能将数组对半分，为了避免数组不够随机带来的效率低下，在进行快速排序之前我们先将数组打乱。

切分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

 * @Author jiaxuehui
 * @Description 快速排序
 * @Date 12:27 PM 24/11/2018
 * @Param
 * @return
 *
 **/
private static<T extends Comparable<T>> int partition(T[] list, int lo, int hi){
    int i = lo, j = hi;
    while (i<j){
        if (list[j].compareTo(list[lo])<=0){
            i++;
            if (list[i].compareTo(list[lo])>=0){
                exchange(list,i,j);
            }
        }
        else
            j--;
    }
    exchange(list,i,lo);
    return i;
}

排序

为了保证效率，我们在进行排序之前应该先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public static<T extends Comparable<T>> void QuickSort(T[] list){
    //random
    List l= new LinkedList();
    for(int i=0;i<list.length;i++){
        l.add(list[i]);
    }
    Collections.shuffle(l);
    Iterator<T> it = l.iterator();
    int i=0;
    while (it.hasNext()){
        list[i] = it.next();
        i++;
    } //打乱

    QuickSort(list,0,list.length-1);
}

public static<T extends Comparable<T>> void QuickSort(T[] list, int lo, int hi){

    if (lo>=hi)
        return;
    int j = partition(list, lo,hi);
    QuickSort(list, lo, j-1);
    QuickSort(list, j+1, hi);
}

三项切分的快速排序

针对有很多重复元素的快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
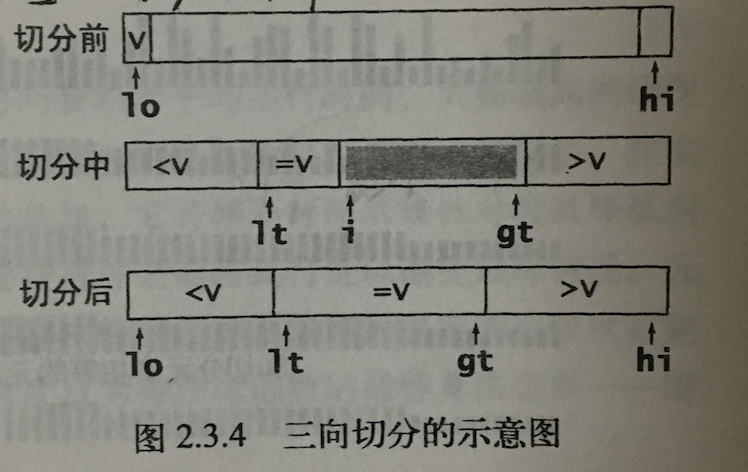
16
public static<T extends Comparable<T>> void QuickSort3Way(T[] list, int lo, int hi){
     if(lo>=hi)
         return;
     int lt = lo,i=lo+1, gt = hi;//lt都小于i，gt都大于i
     while (i<=gt) {
         if (list[i].compareTo(list[lo]) < 0) {  //如果当前元素小于基准，则和lt交换位置，i和lt前进
             exchange(list, lt++, i++);
         } else if (list[i].compareTo(list[lo]) > 0) { //如果当前元素大于基准，则和gt交换位置，gt向左前进
             exchange(list, gt--, i);
         } else i++;
     }

     QuickSort(list,lo, lt-1);
     QuickSort(list,gt+1, hi);

 }

其他提高快排性能的点：

  • 每次选择中轴元素的时，候取中位数，但是牺牲了计算中位数的时间，所以可以每次随机取3个数字计算中位数。
  • 当排序的规模小于一定值是使用插入排序。因为小规模的排序插入排序性能优于快速排序，因为快排使用递归，递归速度很慢，在小规模数据时（例如N<50），可能还不如插入排序快。 （递归效率低是函数调用的开销导致的。在一个函数调用之前需要做许多工作，比如准备函数内局部变量使用的空间、搞定函数的参数等等，这些事情每次调用函数都需要做，因此会产生额外开销导致递归效率偏低，所以逻辑上开销一致时递归的额外开销会多一些）

堆排序（优先队列）

见：优先队列及源码分析+堆排序